2{arc tan ( 1/4) + arc tan (2/9) }=arc cos ( 3/5) || INVERSE CIRCULAR FUNCTIONS

7:46
xy=1+a^2 Then arc tan{1/(a+ x)} + arc tan {1/(b+ x)}= arc tan (1/a) , (a+ b+ 2x ) not equal to 0️⃣
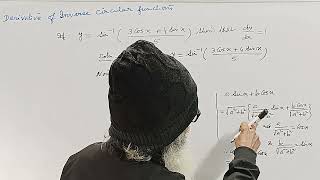
12:49
y= arc sin {(3cosx + 4sinx) /5} Then ( dy/ dx) = 1 || DERIVATIVE | INVERSE CIRCULAR FUNCTIONS

1:19:55
Class X Maths || Similarity || CBSE and Maharashtra State Board Part 2 ||

22:59
The Dome Paradox: A Loophole in Newton's Laws

9:14
y= arc tan { ( 3a^2 x - x^3 ) /a(a^2 - 3x^2 ) } Then (dy/ dx) = ( 3a) /( a^2 + x^2)

15:58
arc tan [(1/√3) tan( x/2) ]=(1/2) arc cos {(1+2cosx) /( 2+cosx) }

13:22
y= arc tan { cosx /( 1+ sin x) }+ sin ( e^x) Then 2( dy/ dx) + 1= 2e^x cos ( e^x)

13:55