xy=1+a^2 Then arc tan{1/(a+ x)} + arc tan {1/(b+ x)}= arc tan (1/a) , (a+ b+ 2x ) not equal to 0️⃣

7:17
arc sin (5/13) - arc tan (5/13) = arc tan ( 5/181) || INVERSE TRIGONOMETRIC FUNCTIONS

14:46
y= arc cos [ x^2 + √ ( 1- x) ( 1- x^3) ] || DIFFERENTIATION

13:12
(a x^3 +3x^2- 3) and (2x^3- 5x+a)Divided by (x-4) |Remainders are A & B respt. With 2A= B Then a= ?
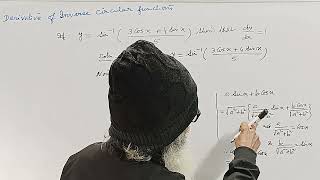
12:49
y= arc sin {(3cosx + 4sinx) /5} Then ( dy/ dx) = 1 || DERIVATIVE | INVERSE CIRCULAR FUNCTIONS
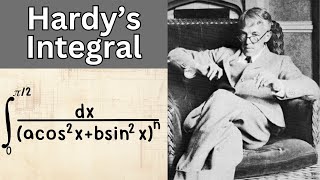
13:47
Hardy's Integral

13:58
y= arc tan{5ax /(a^2- 6 x^2)} Then (dy/dx)= 3a/(a^2 + 9x^2)+ 2a/(a^2+ 4x^2)
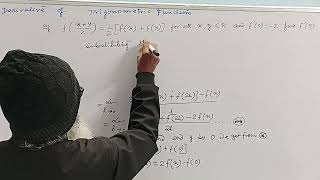
12:42
f{(x+y)/2}=(1/2) [f(x)+f(y)] for all x,y belongs to R and f'(0)= - 2 Then find f'(5) DERIVATIVE

13:22