If f is differentiable, then f is continuous and a little more, Real Analysis II

33:59
The Jacobian Matrix, Real Analysis II

36:25
The Definition of Differentiability (Introduction and Example), Real Analysis II

24:56
Integrate 1/(1+x^3)

24:58
A continuous function on a compact set has compact image, Real Analysis II
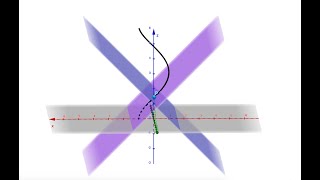
15:30
Osculating & Normal Plane - Example

33:48
Review of Linear Transformations T: R^n to R^m

1:33:00
Olasılık, Rastgelelik ve Matematik Felsefesi – Prof. Dr. Ali Nesin

15:20