A Set is Closed iff it Contains Limit Points | Real Analysis
6:01
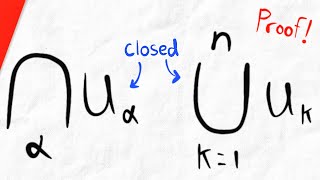
Proof for Unions and Intersections of Closed Sets | Real Analysis

16:14
Real Analysis | The limit point of a set A⊆ℝ

8:19
A Set is Closed if and only if it contains all of it's Limit Points

11:48
All About Closed Sets and Closures of Sets (and Clopen Sets) | Real Analysis

14:23
Real Analysis | Precise definition of a limit.
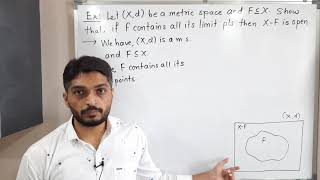
5:08
Metric Spaces | Lecture 50 | If a set contains all its limit points then its Complement is Open.

18:06
402.3A3 Boundary Points of a Set

13:58