Prove that the distinct equivalence classes of an equivalence relation forms a partition of the set

15:44
Matrix representation of relation | Adjacency Matrix | Discrete Mathematics

11:34
Closure of Relation | Reflexive Closure, Symmetric Closure and Transitive Closure | Ganitya

9:32
Equivalence Classes

7:59
Partitions of a Set | Set Theory

7:47
The Union of Two Subspaces is a Subspace iff One is Contained in Other
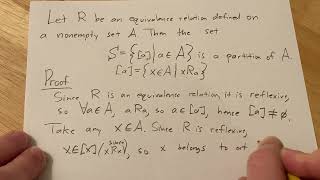
7:15
Important Math Proof: The Set of Equivalence Classes Partition a Set

6:07
Chapter 1: Symmetries, Groups and Actions | Essence of Group Theory

11:06