Cantor set is Compact set and Perfect set | Theorem | Real Analysis | Metric Space | Topology | Msc

16:43
Separated sets | Definition | Examples | Real Analysis | Metric Space | Topology | connectedness

15:46
Closed subset of a compact set is compact | Compact set | Real analysis | Topology | Compactness

12:18
Uncountable set with Lebesgue measure 0 - Cantor Set | Measure Theory

27:32
Perfect subset of R^k is uncountable | Theorem | Real Analysis | Metric Space | point set Topology

13:45
Proof that Nonempty Perfect Set in R^k is Uncountable (feat. Baby Rudin)

35:05
Theorem of connectedness | Connectedness | Real analysis | Metric space | topology | Compactness
15:37
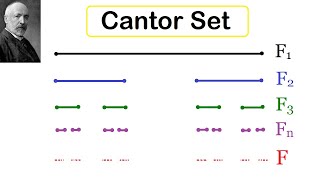
Cantor set

23:53