y= arc tan [x/{1+√(1- x^2) }] + sin [2arctan √{( 1- x) /(1+x) }] Then (dy/ dx) = (1-2x) /2√(1- x^2)
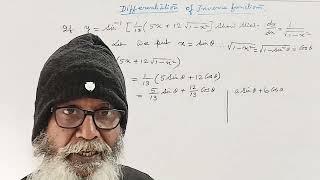
10:47
y=arc sin(1/13){5x+12√(1- x^2)}Then (dy/dx)=1/√(1- x^2)|| DERIVATIVE ,INVERSE TRIGONOMETRIC FUNCTION

13:11
MHF4U 1.9a Instantaneous Rate of Change

2:37
` int _(0)^(a) (xdx)/(sqrt(a^(2)+x^(2)) )` is equal to
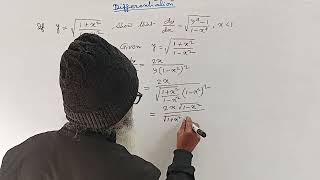
18:29
y= √{( 1+ x^2) /(1- x^2) } Then (dy/ dx) = √{( y^4-1) /(1- x^4) } , x less than 1 || DIFFERENTIATION

7:39
VALUE of arc cos x+ arc cos [x/2+ √(3-3x^2)/2] , 1/2 less than or equal to x less than or equal to 1
16:15
Pouvez-vous trouver X ? - Question d'examen d'entrée à Harvard
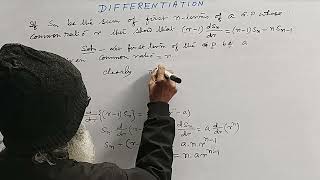
13:13
DERIVATIVE || Sn -Sum of 1st n terms,r the Common Ratio of a G.P Then (r-1)(dSn/dr)=(n-1) Sn - nSn-1

32:36