If a and b are two elements of a.finite group G s.t.ab=ba and (o(a),o(b))=1 then o(ab)=o(a)o(b)

10:05
#04 trick of abstarct algebra | If in a group G , a^5=e ,aba^-1 =b^2 , then order of b is

20:00
G is group and a,b be elements of G such that (o(a),o(b))=1 and ab=ba then o(ab)=o(a)o(b).
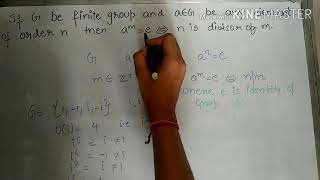
8:36
if G be finite group and a be any element of G s.t. o(a)=n them a^m=e iff n|m

15:23
Order of an element divides order of the group | order of a group and order of an element | cosets
45:24
Why you can't solve quintic equations (Galois theory approach) #SoME2

6:50
In a finite group order of every element exist

26:12
How to Remember Everything You Read

12:51