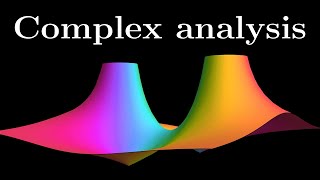
Complex integration, Cauchy and residue theorems | Essence of Complex Analysis #6
3:55
Why care about complex analysis? | Essence of complex analysis #1

28:33
What do complex functions look like? | Essence of complex analysis #4

8:27
Simple Interest Formula
52:49
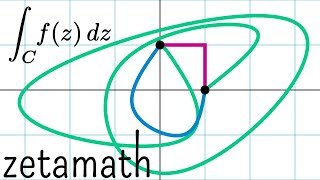
Complex Integration and Finding Zeros of the Zeta Function

43:26
How Can Light Travel Everywhere at Once? Feynman’s Path Integral Explained
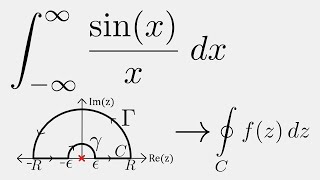
17:43
Complex Analysis: Integral of sin(x)/x using Contour Integration
45:24
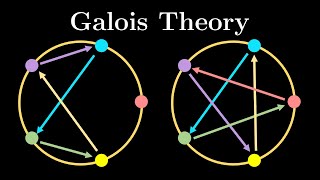
Why you can't solve quintic equations (Galois theory approach) #SoME2

24:47