2 (arc sin x)= arc sin {2x √(1- x^2)} || arc sin x means sin inverse x || INVERSE CIRCULAR FUNCTIONS
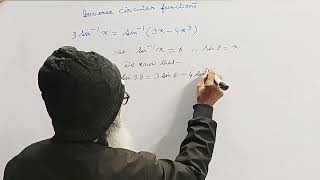
3:44
3( arc sin x) = arc sin ( 3x- 4x^3) || arc sin x means sin inverse x || INVERSE CIRCULAR FUNCTIONS

7:32
arc sin x + arc cos x=π/2 || INVERSE CIRCULAR FUNCTIONS

13:22
y= arc tan { cosx /( 1+ sin x) }+ sin ( e^x) Then 2( dy/ dx) + 1= 2e^x cos ( e^x)
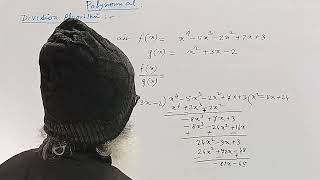
13:28
POLYNOMIAL || DIVISION of TWO POLYNOMIALS May or may not be a POLYNOMIAL || Explained With Example

22:54
PRINCIPAL VALUE of arc cos ( - 1/√2 ) || PRINCIPAL VALUE || INVERSE TRIGONOMETRIC FUNCTIONS

14:46
y= arc cos [ x^2 + √ ( 1- x) ( 1- x^3) ] || DIFFERENTIATION

15:53
Value of arc sin (sin10) || Concept of General solution of Trigonometric Equation ||
21:31