Projections of Probability Distributions: A Measure-Theoretic Dvoretzky Theorem

58:42
Sharp Isoperimetric Inequalities for Affine Quermassintegrals

1:10:16
Poincaré's Probability

1:02:41
Mod-01 Lec-01 Discrete probability distributions (Part 1)
26:34
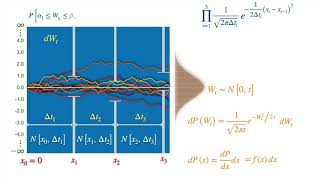
Simplified: Girsanov Theorem for Brownian Motion (Change of Probability Measure)
23:15
How Large is the Norm of a Random Matrix?
34:43
Michael Cohen and High-dimensional Probability

1:00:28
Sudeep Kamath : Concentration of Measure - 1

52:11