Integration by (u-)substitution

30:31
Intuition for integration techniques

31:20
Integration by parts
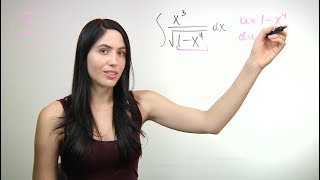
25:48
How to Integrate Using U-Substitution (NancyPi)

27:57
Arithmetic and operations
29:40
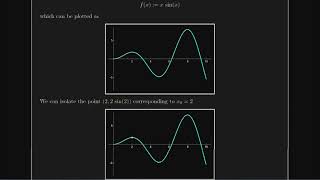
The (continuous) derivative

20:37
Integrate x^-x dx

16:59
integration by parts, DI method, VERY EASY

32:12