if G be finite group and a be any element of G s.t. o(a)=n them a^m=e iff n|m

12:57
If you're ambitious but lazy, please watch this video...
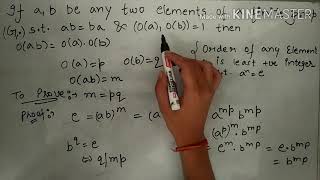
13:40
If a and b are two elements of a.finite group G s.t.ab=ba and (o(a),o(b))=1 then o(ab)=o(a)o(b)

10:17
If G be any group and a belongs to G be any element then o(a^k)=o(a)/(o(a),k)

13:46
Semigroup and it's theorm

12:38
A finite semigroup becomes group when both cancellation laws hold in it.

12:16
7 Outside The Box Puzzles

13:28
In a group of even order the number of elements of order 2 are odd

9:14