Compact Sets are Closed and Bounded

12:45
AM-GM Inequality | Arithmetic Mean Geometric Mean Inequality

13:58
Open Covers, Finite Subcovers, and Compact Sets | Real Analysis

20:47
The Concept So Much of Modern Math is Built On | Compactness
6:42
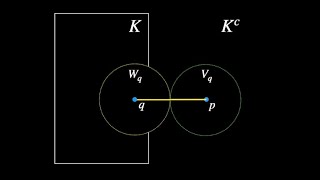
Rudin Illustrated Proof: Compact subsets of metric spaces are closed.
27:20
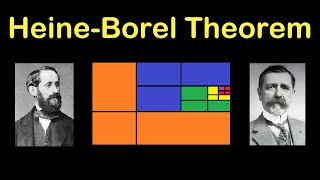
Heine Borel Theorem
10:56
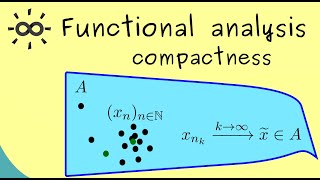
Functional Analysis 16 | Compact Sets

45:19
Group Homomorphisms: What Are They Really?

27:33