Montrer que f est dérivable en un point

8:00
Montrer que f n'est pas dérivable en un point

22:26
Fonction dérivée et tangente

7:17
Déterminer les variations d'une fonction (1) - Seconde

6:46
Domaine de DÉFINITION et domaine de DÉRIVABILITÉ - Première
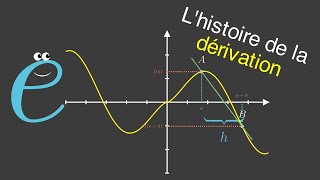
14:05
Comment comprendre FACILEMENT les dérivées

10:40
VARIATIONS D’UNE FONCTION - Définition

9:58
Calculer le nombre dérivé (1) - Première

1:33:38